并查集详解与应用

发表于 更新于 分类于

并查集是一种树形的数据结构，顾名思义，它用于处理一些不交集的 合并 及 查询 问题。 它支持两种操作：查询、合并。查询用于查找元素在哪个子集中，合并用于将两个子集合并成一个。

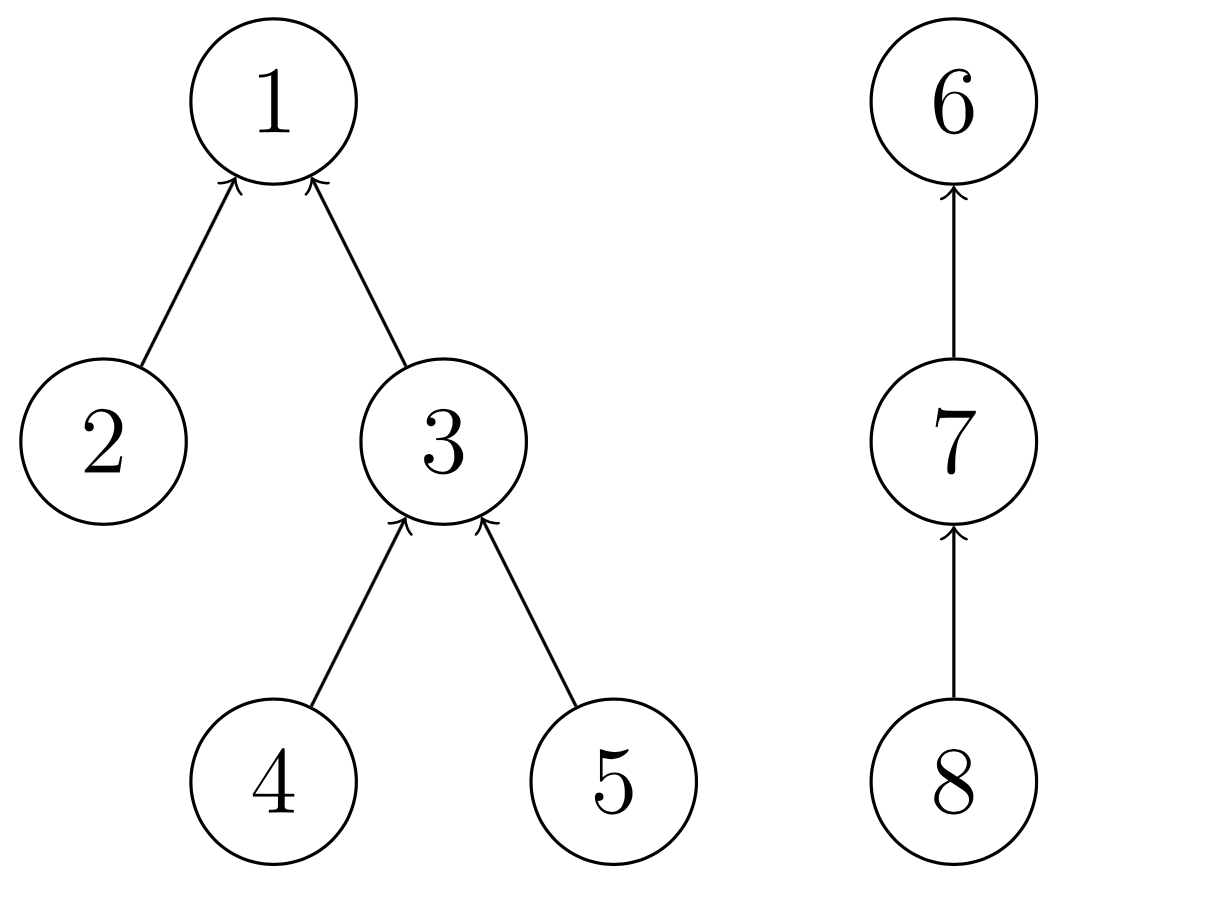
disjoint-set

这是一个什么样的结构体？一个 int[] fa 即可。每个结点都只有一个父节点， fa[3] == 1，表示的是 3 号结点的父节点为 1，特别的，祖父结点的父节点为本身。

初始化

首先是初始化，每个结点的父节点设置为自己。

1
2
3
4
5
6
7
public void init(int n) {
    fa = new int[n];
    // 每个结点为一个子集
    for(int i = 0; i < n; i++) {
        fa[i] = i;
    }
}

查询

查询操作是查找一个结点的祖宗结点的过程，简单递归即可。

1
2
3
4
5
6
public void find(int node) {
    if(fa[node] == node) {
        return node;
    }
    return find(fa[node]);
}
路径压缩

我们在查询之后，得到了某个结点的祖宗结点。如果不做优化，下次查询该结点可能还需要很多步，纯属浪费，我们可以直接将该结点，提到祖宗结点的下一层，下次查询非常快。

路径压缩

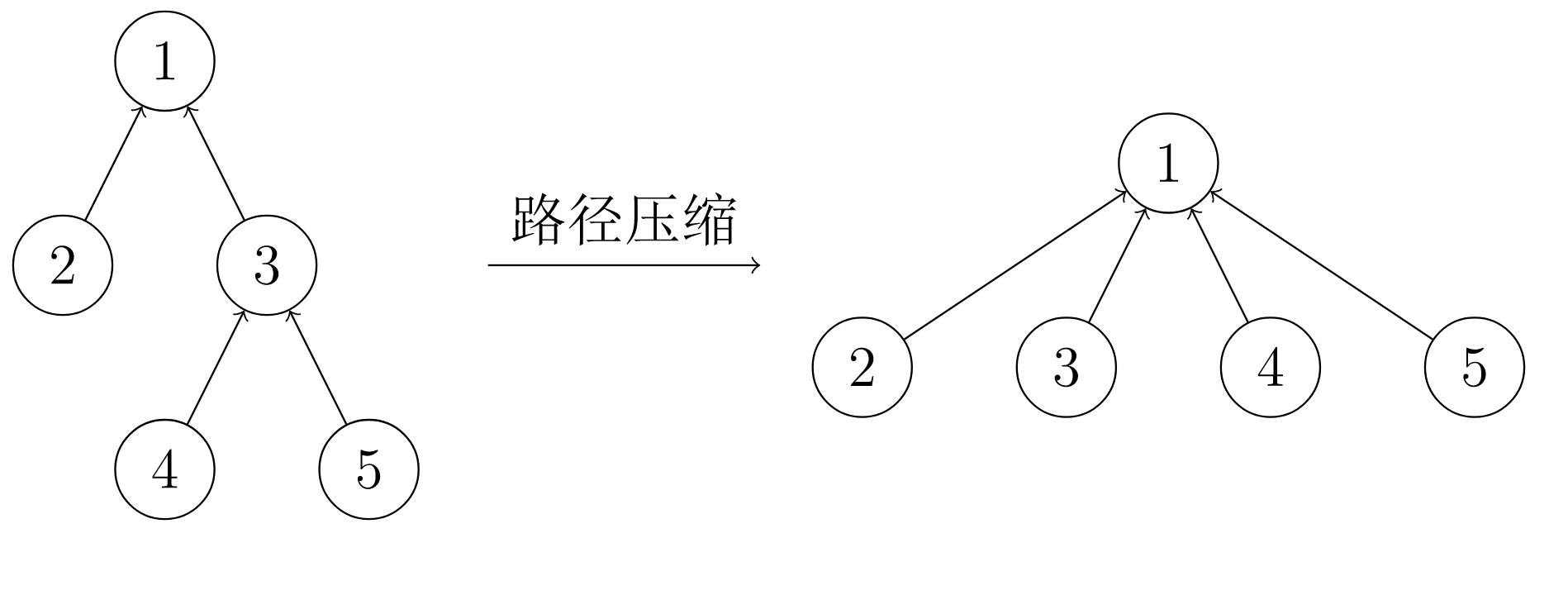
啰嗦写法，但易懂。

1
2
3
4
5
6
7
8
9
public void find(int node) {
    if(fa[node] == node) {
        return node;
    }
    int p = find(fa[node]);
    // 将该结点的父节点直接设置为祖宗结点
    fa[node] = p;
    rerturn p;
}

简单写法。

1
2
3
4
5
6
public void find(int node) {
    if(fa[node] != node) {
        fa[node] = find(fa[node]);
    }
    rerturn fa[node];
}

合并

1
2
3
4
5
6
public void union(int x, int y) {
    x = find[x];
    y = find[y];
    // 将 x 的祖先变成 y 的儿子
    fa[x] = y;
}

应用

哪些问题可以使用并查集来解决？

  1. 查找元素属于哪个集合
  2. 判断两个元素是否在同一个集合
  3. 计算集合的个数，森林中子森林的个数。

心得

并查集一般都是使用 int [] 来存储数据，但一些情况下题目提供的是字符串或者其它对象，我们需要将这些元素映射到数组 int [] 中，同时使用一个 Map 来存储原字符串和 int [] 中下标的对应关系，即存下标。可以看例题 399 题，「除法求值」。

另外还有一些题目，不再是简单的并查集，并查集中除了 fa[] 数组，还需要维护一些其他数据，这就r是带权并查集，还是可以看「除法求值」这一题。